octavo año educacion estetica

Tarea para el 16 y 17 de Abril del 2016


los cuadriláteros  definición elementos y clasisficación

Cuadrilátero

Para el núcleo conspirativo que participó en el golpe de Estado de Primo de Rivera de 1923, véase Cuadrilátero (Dictadura de Primo de Rivera).

Clases de cuadriláteros convexos.

Un cuadrilátero es una figura que tiene cuatro lados. Los cuadriláteros pueden tener distintas formas, pero todos ellos tienen cuatro vértices y dos diagonales, y la suma de sus ángulos internos siempre es 360°.

Un cuadrilátero se llama convexo si se encuentra en un mismo semiplano respecto a la recta que contiene cualquiera de sus lados. Los segmentos que unen los vértices opuestos del cuadrilátero se denominan diagonales.¹

Todos los cuadriláteros son cuadrángulos, ya que esta definición se aplica a lospolígonos de cuatro ángulos.

Propiedades[editar]

• Las diagonales de un cuadrilátero convexo se cortan; cuando el cuadrilátero no es convexo, las diagonales no se intersecan.
• La suma de los ángulos de un cuadrilátero convexo es 360º o 2π radianes.
• Todo cuadrilátero convexo puede expresarse como la unión de dos triángulos con lado común una de la diagonales.
• Un segmento que pasa por la intersección de las diagonales de un cuadrilátero y une dos lados opuestos determina dos cuadriláteros con un lado común.²
• En un cuadrilátero inscrito en una circunferencia la suma de sus ángulos opuestos es igual a 180º.
• Sea ABCD un cuadrilátero inscrito, AB su diámetro, entonces las proyecciones de sus lados AD y BC sobre la recta CD son iguales.
• El área de un cuadrilátero inscrito se obtiene con la fórmula  donde a, b, c, d son los lados y p es el semiperímetro.
• Si 2α es la suma de dos ángulos opuestos de un cuadrilátero circunscrito, A su área, a,b, c, d sus lados entonces cabe la fórmula A² = (abcd)sen²α.³
• Si las diagonales de un cuadrilátero convexo lo divide en cuatro triángulos y los radios de la circunferencias en estos triángulos son iguales, entonces dicho cuadrilátero es un rombo.
• Si se unen con cuatro segmentos los puntos medios de todos los lados de un cuadrilátero, entonces dichos segmentos forman un paralelogramo.
• Si en el cuadrilátero ABCD los radios de las circunferencias inscritas en los triángulos ABC, BCD, CDA, DAB son iguales, entonces dicho cuadrilátero es un rectángulo.
• Si las diagonales de un cuadrilátero lo dividen en cuatro triángulos de igual perímetro, entonces el cuadrilátero original es un rombo.⁴
• Si un cuadrilátero está inscrito entonces la suma de sus ángulos opuestos es 180º.
• Si un cuadrilátero está circunscrito entonces la suma de sus lados opuestos con iguales. .⁵

• Para un cuadrilátero convexo se cumple  donde  son los lados; ,las diagonales y m, la longitud del segmento que une los puntos medios de las diagonales.
• También se verifica:  donde  son las diagonales y  son los segmentos que unen los puntos medios de lados opuestos.⁶

Elementos de un cuadrilátero[editar]

Los elementos de un cuadrilátero son los siguientes:

• 4 vértices: puntos de intersección de los lados que conforman el cuadrilátero.

• 4 lados: segmentos que unen los vértices contiguos.

• 2 diagonales: segmentos cuyos extremos son dos vértices no contiguos.

• 4 ángulos interiores: el determinado por dos lados contiguos.

• 4 ángulos exteriores: el determinado por la prolongación de uno de los lados sobre un vértice y el contiguo en el mismo vértice.

Clasificación de los cuadriláteros[editar]

Deltoides

Tipos de Paralelogramos

Los cuadriláteros se clasifican según el paralelismo de sus lados, sus longitudes y sus ángulos interiores:

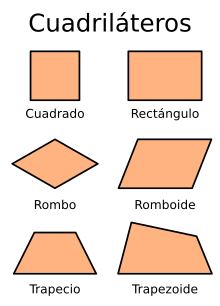
1. Paralelogramo: sus lados opuestos son paralelos.

• Cuadrado: todos sus lados son iguales, todos sus ángulos interiores son rectos, sus diagonales son iguales y perpendiculares entre si, tiene una circunferencia inscritas y otra circunscrita.
• Rombo: todos sus lados son iguales, cada par de ángulos agudos y obtusos son opuestos, sus diagonales son distintas y perpendiculares entre sí, son bisectrices, tiene una circunferencia inscrita.
• Rectángulo: sus lados opuestos son iguales dos a dos y los paralelos, todos sus ángulos interiores son rectos, sus dos diagonales son iguales pero no son perpendiculares entre si y tiene una circunferencia circunscrita.
• Romboide: sus lados opuestos son iguales dos a dos, cada par de ángulos agudos y obtusos son opuestos, sus dos diagonales son de distinta longitud y no son perpendiculares entre sí.

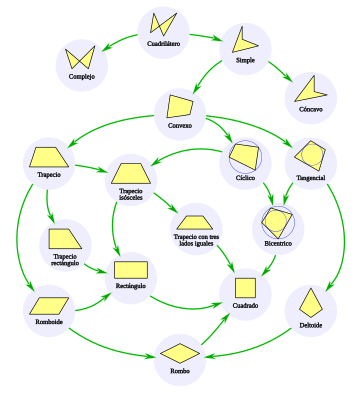
Taxonomía de los cuadriláteros[editar]

En el gráfico ilustrativo de la taxonomía de los cuadriláteros se pasa de las definiciones más generales a las más específicas siguiendo el sentido de las flechas.

Así se parte de un cuadrilátero definido como un polígonocerrado de cuatro lados, sin más restricciones, para diferenciar los cuadriláteros compuestos de los simples.

En un cuadrilátero complejo, dos de sus lados se cortan. En uno simple los lados no se cruzan.

Los cuadriláteros simples se dividen en:

• Cóncavos. En un cuadrilátero cóncavo al menos uno de sus ángulos interiores mide más de 180°.
• Convexos. Un cuadrilátero convexo no tiene ángulos interiores que midan más de 180°. Los convexos se subdividen en:

1. Cuadrilátero cíclico, si se puede trazar una circunferencia que pase por sus vértices.
2. Cuadrilátero tangencial, si se puede trazar unacircunferencia tangente a cada uno de sus lados.
3. Trapecios, si tienen dos lados paralelos. Se diferencian:
   1. Romboide, como caso más general de paralelogramo, si los lados son paralelos dos a dos.
   2. Trapecio rectángulo, que tiene un lado perpendicular a sus bases.
   3. Trapecio isósceles, cuyos lados no paralelos son de igual medida. Este trapecio también es cíclico.

A un cuadrilátero que al mismo tiempo sea cíclico y tangencial se le denomina cuadrilátero bicéntrico. El deltoide es tangencial con dos pares de lados iguales.

Un caso particular de trapecio isósceles es cuando la longitud de una de las bases es igual que la de sus lados, por lo cual se configura un trapecio de tres lados iguales.